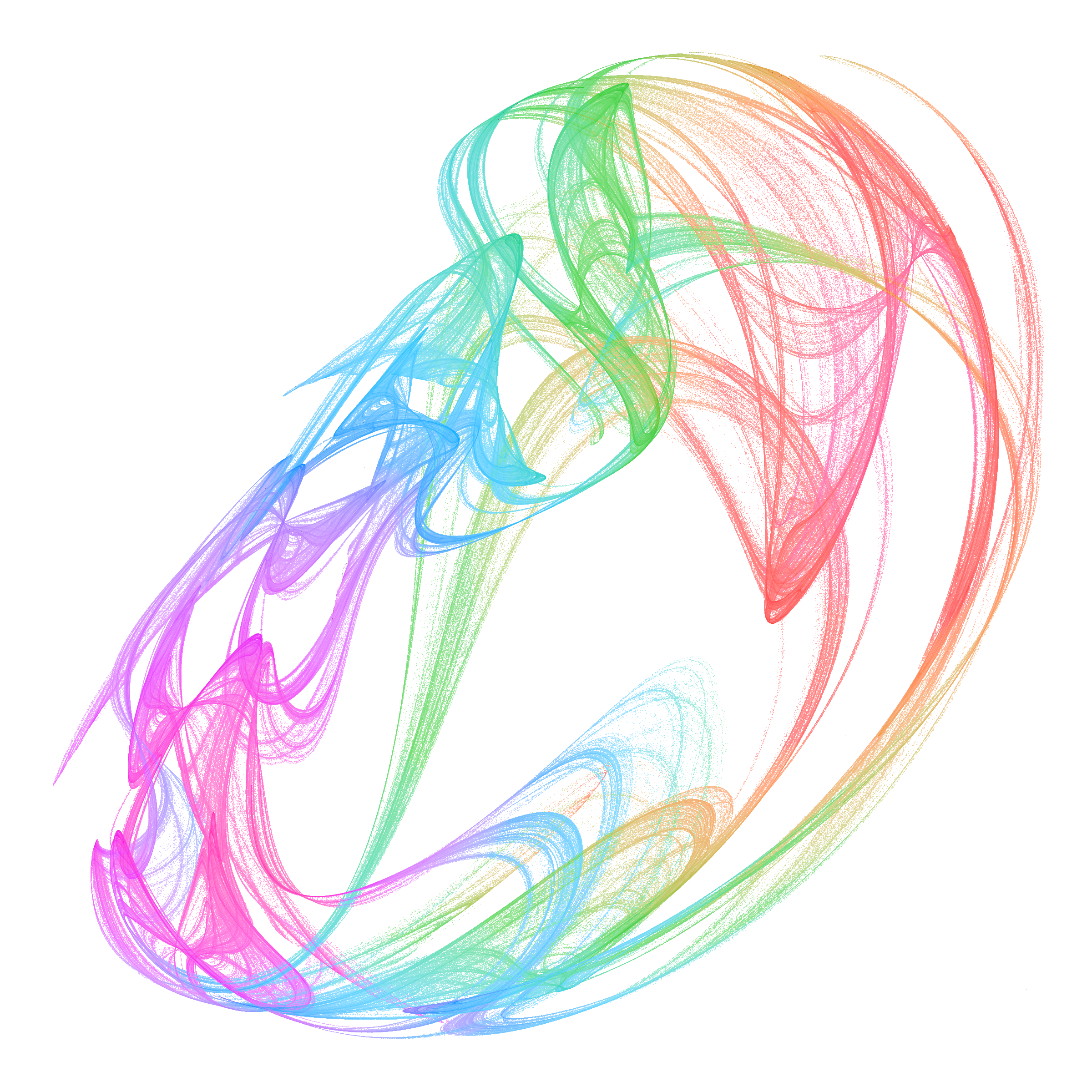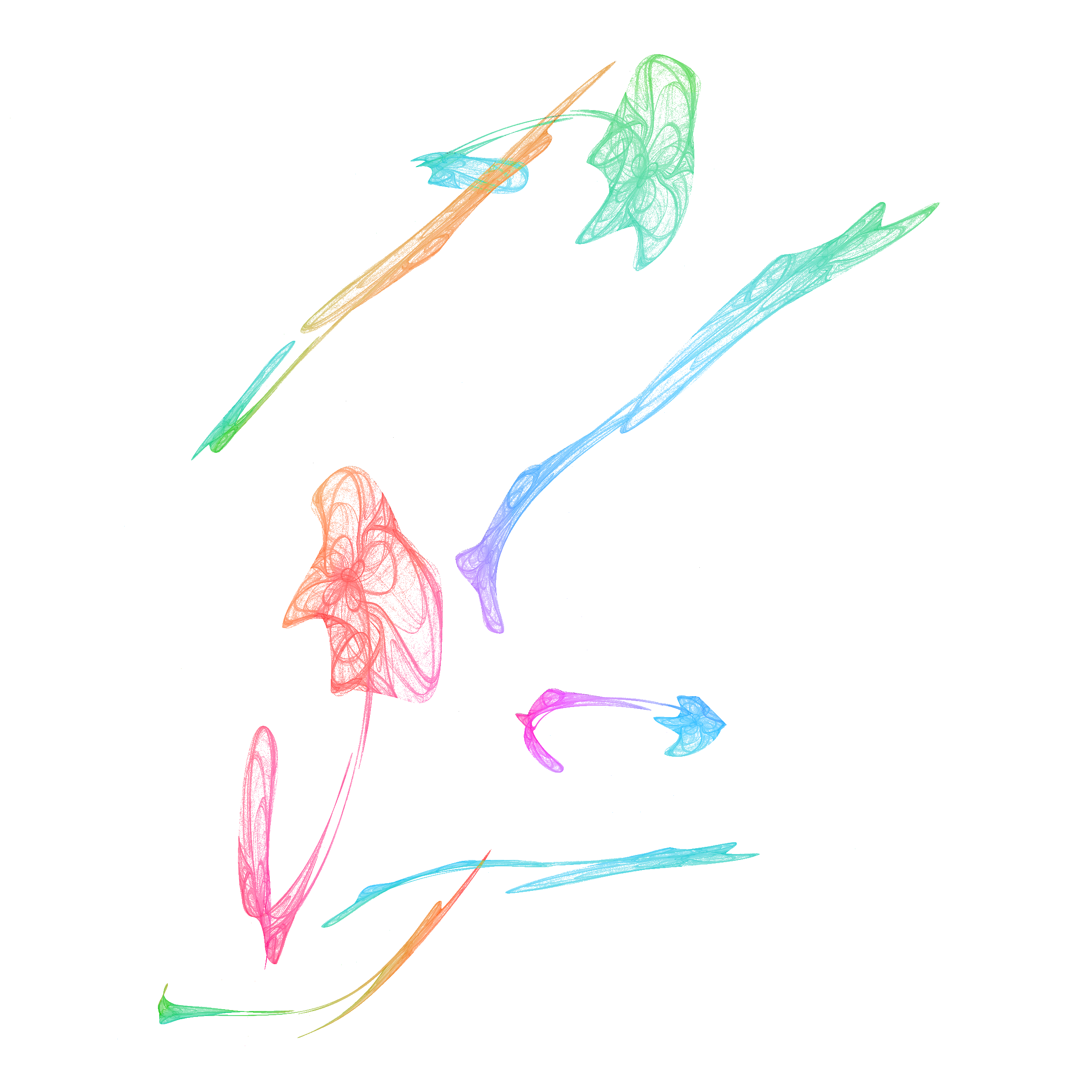Finding Flowers In Chaos
Strange attractors, produce some incredible shapes from a very simple process. A mathematical transformation is iteratively applied to a point. For some transformations, the value/location of the point will be constant, or move between a small number of fixed values. These are attractors. For a rarer set of transformations the point will move between a fractal set of values, these are strange attractors. They can be beautiful in very surprising ways.
This article and the code that generates the attractors is inspired by the 1993 book Strange Attractors: Creating Patterns in Chaos by Julien C. Sprott — which gives a much more eloquant and complete description of the topic than I do here.
How These are Generated
The components of a point \(P\) at \(n\) are \( \left( x_n , y_n , z_n \right) \)
If we compute the 2nd degree polynomial transformation, we can expand this to 10 terms (including a constant term) \( \left( x_n^2 ,y_n^2 ,z_n^2 ,x_n y_n ,y_n z_n ,z_n x_n ,x_n ,y_n ,z_n ,1 \right) \)
We can then use that multiply a constant 10×3 matrix \(\mathbf{A}\)
$$ \begin{pmatrix} a_{00} & a_{01} & a_{02} & ... & a_{09} \\ a_{10} & a_{11} & a_{12} & ... & a_{19} \\ a_{20} & a_{21} & a_{22} & ... & a_{29} \\ \end{pmatrix} $$
And generate a new point whose components are
$$ \begin{pmatrix} a_{00} x_n^2 + a_{01} y_n^2 + a_{02} z_n^2 + a_{03} x_n y_n + a_{04} y_n z_n + a_{05} z_n z_n + a_{06} x_n + a_{07} y_n + a_{08} z_n + a_{09} \\ a_{10} x_n^2 + a_{11} y_n^2 + a_{12} z_n^2 + a_{13} x_n y_n + a_{14} y_n z_n + a_{15} z_n z_n + a_{16} x_n + a_{17} y_n + a_{18} z_n + a_{19} \\ a_{20} x_n^2 + a_{21} y_n^2 + a_{22} z_n^2 + a_{23} x_n y_n + a_{24} y_n z_n + a_{25} z_n z_n + a_{26} x_n + a_{27} y_n + a_{28} z_n + a_{29} \end{pmatrix} $$
We can then perform this iteratively as many times as we care to. It's fairly clear that for most values of \(\mathbf{A}\) that this will diverge, and that for another large set it will converge on a single value. We are interested in the cases where it doesn't do either of those things.
When it converges on a small number of points, they are Attractors when it converges on a set of points with a fractal dimension they are Strange Attractors.
If \(\mathbf{A}\) aren't interesting, how do we find the interestring ones? We take advantage of the crazy ability of computers to process numbers, and just try over and over again until we find something.
How We Find Interesting Attractors
The approach is to search for these by randomly generating sets of 30 constants in the interval \( \left[ -1.2, 1.2 \right] \) quantized to the nearest \( 0.1 \). This gives a state space of \( 25^30 \) to explore, or \( \approx 8.67 \times {10}^{41} \) different combinations.
To check if a parameter set is interesting we use a couple of heuristics
If the sum of the absolute components of the point is greater than an arbitrary limit. \( \left|x_n\right| + \left|y_n\right| + \left|z_n\right| > 1,000,000 \) then we assume that the series is diverging
We calculate the mean of the log of of the distance between successive points $$ \frac{\sum_{i=1}^n{\log\left(P_i - P_{i-1}\right)^2}}{n} $$ if that value becomes too small then we assume that the series is converging
The iteration containing the previous checks is run 11,000 times. The first 1,000 iterations are ignored, to allow the system to stabilize, then the subsequent 10,000 iterations are used to compute the bounds of the three components.
Given those bounds, and assuming that neither other check has failed, then we divide the bounded space (in x and y) into an 8×8 grid, repeat the iteration and count the hits in each bucket. If more than half of the buckets are empty, then we consider this to be uninteresting.
Where are the Flowers?
The simple answer is, "I don't know", but sometimes you stumble across wonder
You can explore these yourself at pollrobots.com/strange.html